Lasso (l1 penalty VS Ridge (l2 penalty)

Ridge and Lasso are forms of regularized linear regressions. The regularization can also be interpreted as prior in a maximum a posterior estimation method. Ridge and Lasso regression use two different penalty functions. Ridge uses l2, which is the sum of the squares of the coefficients. And for Lasso is the L1 norm, which is the sum of the absolute values of the coefficients.

 The ridge (L2) regression can't zero coefficients out, so we either select all the coefficients or none of them, whereas Lasso (L1) does both parameter shrinkage and variable selection automatically because it zero out the coefficient of collinear variables, which mean it can help to select the variables out of given n variables while performing lasso regression. 

 We will continue to talk about the difference between L1 and L2 norm. While practicing machine learning, you may have come upon a choice of L1 and L2. Usually the two decisions are :1) L1-norm vs L2-norm loss function; and 2) L1-regularization vs L2-regularization.

  L1-regularization will move any weight towards 0 with the same step size, regardless the weight's value. In contrast, you can see that the L2 gradient is linearly decreasing towards 0 as the weight goes towards 0. Therefore, L2-regularization will also move any weight towards 0, but it will take smaller and smaller steps as a weight approaches 0.
More explanation about l1 and l2 please look at here:
http://www.chioka.in/differences-between-l1-and-l2-as-loss-function-and-regularization/

https://stats.stackexchange.com/questions/45643/why-l1-norm-for-sparse-models

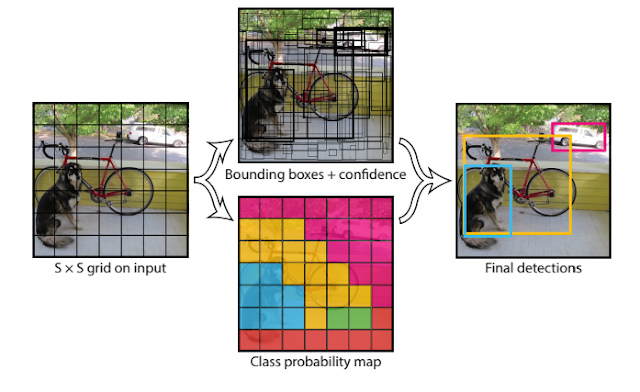
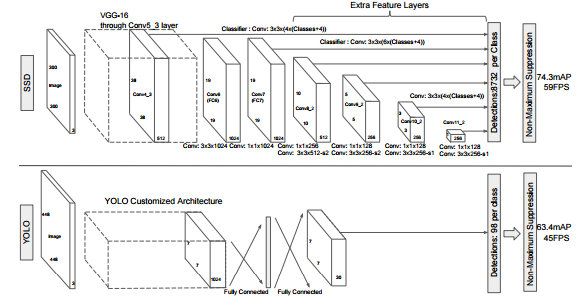
Comments

Post a Comment

Popular posts from this blog

The difference between autoencoders and a restricted Boltzmann machine?

Image
Autoencoder is a simple 3-layer neural network where output units are directly connected back to input units. E.g. in a network like this: output[i] has edge back to input[j] for every hidden node. Usually, the number of hidden units is much less than the number of visible ones. As a result, when you pass data through such a network, it first encodes input vector to fit a smaller representation and then decodes it back. The task of the training is to minimize an error of reconstruction or find the most efficient compact representation for input data. The AEs (Autoencoders) are similar to PCA and can be used to dimension reduction. The hidden layer decoded features can be used as input features for downstream classification or another AE. RBM  is a  generative   artificial neural network  that can learn a  probability distribution  over a set of inputs.  RBMs are a variant of  Boltzmann machines , with the restriction that their  neurons  must form a  bipartite graph :  there are
Read more

SSD: Single Shot MultiBox Detector

Image
SSD is the extension or updating version of YOLO. Compared with YOLO: 1 SSD use the multi-scale feature maps for detection, but the YOLO only use one scale for detection. 2 Before the decision layer, the YOLO use the fully connected layer for detection, but the SSD use the convolution filter for detection, which can improve the final detection performance. 3 Default boxes and aspect ratios. there are a set of default bounding boxes with each feature map cell for multiple feature maps at the top of the network. R-CNN: Selective Search Region Proposals; SVM classification Fast R-CNN: Selective Search Region Proposals; Shared computation by using SSP. Faster R-CNN: Region Proposal Network OverFeat VS SSD: If the SSD only use one default box per location from the topmost feature map, the SSD would have similar architecture to OverFeat. YOLO VS SSD: If use the whole topmost feature map and add a fully-connected layer for predictions instead of convolutional predictors, it'
Read more

You Only Look Once

Image
Title: You Only Look Once: Unified, Real-Time Object Detection YOLO is a new approach for object detection. You only need run a single CNN on the image once and make the decision for each grid. Instead of using the sliding windows or region proposes. the YOLO proposed to divide the image to S*S grid and predict each grid with regression. Contribution: The traditional model will do a classification for each proposal or sliding window, but the proposed YOLO divide the image to S*S grid and train a regression model. The ground truth target vector has the dimension of S*S*(B*5+C). Each grid cell predicts B bounding boxes and confidence scores for those boxes. The confidence score reflects how confidence the current grid contain the object and also how accurate it thinks the box is that it predicts. Network: The network has 24 constitutional layers followed by 2 fully connected layers. There are four 2*2 max-pooling layers with stride 2. Instead of inception modules used by Goog
Read more